API docs

The list below summarizes classes and functions exposed to the user, ie. imported by:

from ffnet import *

ffnet(conec[, lazy_derivative])	Feed-forward neural network main class.
mlgraph(arch[, biases])	Creates standard multilayer network architecture.
tmlgraph(arch[, biases])	Creates multilayer network full connectivity list.
imlgraph(arch[, biases])	Creates multilayer architecture with independent outputs.
savenet(net, filename)	Dumps network to a file using cPickle.
loadnet(filename)	Loads network pickled previously with savenet.
exportnet(net, filename[, name, lang, ...])	Exports network to a compiled language source code.
readdata(filename, **kwargs)	Reads arrays from ASCII files.

pikaia(ff, n[, ff_extra_args, individuals, ...])

Pikaia version 1.2 - genetic algorithm based optimizer.

Architecture generators

ffnet.mlgraph(arch, biases=True)

Creates standard multilayer network architecture.

Parameters:

arch : tuple

Tuple of integers - numbers of nodes in subsequent layers.

biases : bool, optional

Indicates if bias (node numbered 0) should be added to hidden and output neurons. Default is True.

Returns:

conec : list

List of tuples – network connections.

Examples:

Basic calls:

>>> from ffnet import mlgraph
>>> mlgraph((2,2,1))
[(1, 3), (2, 3), (0, 3), (1, 4), (2, 4), (0, 4), (3, 5), (4, 5), (0, 5)]
>>> mlgraph((2,2,1), biases = False)
[(1, 3), (2, 3), (1, 4), (2, 4), (3, 5), (4, 5)]

Exemplary plot:

from ffnet import mlgraph, ffnet
import networkx as NX
import pylab

conec = mlgraph((3,6,3,2), biases=False)
net = ffnet(conec)
NX.draw_graphviz(net.graph, prog='dot')
pylab.show()

(Source code, png, hires.png, pdf)

ffnet.tmlgraph(arch, biases=True)

Creates multilayer network full connectivity list.

Similar to mlgraph, but now layers are fully connected with all preceding layers.

Parameters:

arch : tuple

Tuple of integers - numbers of nodes in subsequent layers.

biases : bool, optional

Indicates if bias (node numbered 0) should be added to hidden and output neurons. Default is True.

Returns:

conec : list

List of tuples – network connections.

Examples:

Basic calls:

>>> from ffnet import tmlgraph
>>> tmlgraph((2,2,1))
    [(0, 3),
    (1, 3),
    (2, 3),
    (0, 4),
    (1, 4),
    (2, 4),
    (0, 5),
    (1, 5),
    (2, 5),
    (3, 5),
    (4, 5)]
>>> tmlgraph((2,2,1), biases = False)
[(1, 3), (2, 3), (1, 4), (2, 4), (1, 5), (2, 5), (3, 5), (4, 5)]

Exemplary plot:

from ffnet import tmlgraph, ffnet
import networkx as NX
import pylab

conec = tmlgraph((3, 8, 3), biases=False)
net = ffnet(conec)
NX.draw_graphviz(net.graph, prog='dot')
pylab.show()

(Source code, png, hires.png, pdf)

ffnet.imlgraph(arch, biases=True)

Creates multilayer architecture with independent outputs.

This function uses mlgraph to build independent multilayer architectures for each output neuron. Then it merges them into one graph with common input nodes.

Parameters:

arch : tuple

Tuple of length 3. The first element is number of network inputs, last one is number of outputs and the middle one is interpreted as the hidden layers definition (it can be an integer or a list – see examples)

biases : bool, optional

Indicates if bias (node numbered 0) should be added to hidden and output neurons. Default is True.

Returns:

conec : list

List of tuples – network connections.

Raises:

TypeError

If arch cannot be properly interpreted.

Examples:

The following arch definitions are possible:

>>> from ffnet import imlgraph
>>> arch = (2, 2, 2)
>>> imlgraph(arch, biases=False)
    [(1, 3),
    (2, 3),
    (1, 4),
    (2, 4),
    (3, 5),
    (4, 5),
    (1, 6),
    (2, 6),
    (1, 7),
    (2, 7),
    (6, 8),
    (7, 8)]

In this case two multilayer networks (for two outputs) of the architectures (2,2,1), (2,2,1) are merged into one graph.

>>> arch = (2, [(2,), (2,2)], 2)
>>> imlgraph(arch, biases=False)
    [(1, 3),
    (2, 3),
    (1, 4),
    (2, 4),
    (3, 5),
    (4, 5),
    (1, 6),
    (2, 6),
    (1, 7),
    (2, 7),
    (6, 8),
    (7, 8),
    (6, 9),
    (7, 9),
    (8, 10),
    (9, 10)]

I this case networks of the architectures (2,2,1) and (2,2,2,1) are merged.

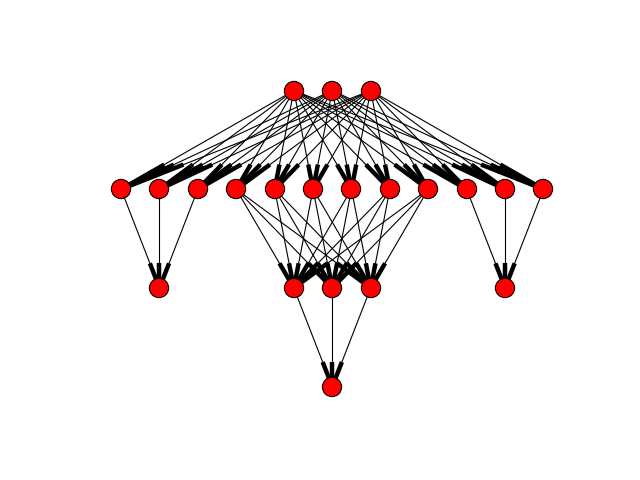
Exemplary plot:

from ffnet import imlgraph, ffnet
import networkx as NX
import pylab

conec = imlgraph((3, [(3,), (6, 3), (3,)], 3), biases=False)
net = ffnet(conec)
NX.draw_graphviz(net.graph, prog='dot')
pylab.show()

(Source code, png, hires.png, pdf)

Main ffnet class

class ffnet.ffnet(conec, lazy_derivative=True)

Feed-forward neural network main class.

Parameters:

conec : list of tuples

List of network connections

lazy_derivative : bool

If True all data necessary for derivatives calculation (see ffnet.derivative method) are generated only on demand.

Returns:

net

Feed forward network object

Raises:

TypeError

If conec is not directed acyclic graph

Instance attributes:  

conec : array

Topologically sorted network connections

weights : array

Weights in order of topologically sorted connections

renormalize : bool

If True normalization ranges will be recreated from training data at next training call.

Default is True

Examples:

>>> from ffnet import mlgraph, ffnet
>>> conec = mlgraph((2,2,1))
>>> net = ffnet(conec)

See also:

mlgraph, tmlgraph, imlgraph

call(inp)

Calculates network answer to given input.

Parameters:

inp : array

2D array of input patterns (or 1D for single pattern)

Returns:

ans : array

1D or 2D array of calculated network outputs

Raises:

TypeError

If inp is invalid

derivative(inp)

Returns partial derivatives of the network’s output vs its input.

For each input pattern an array of the form:

| o1/i1, o1/i2, ..., o1/in |
| o2/i1, o2/i2, ..., o2/in |
| ...                      |
| om/i1, om/i2, ..., om/in |

is returned.

Parameters:

inp : array

2D array of input patterns (or 1D for single pattern)

Returns:

ans : array

1D or 2D array of calculated network outputs

Examples:

>>> from ffnet import mlgraph, ffnet
>>> conec = mlgraph((3,3,2))
>>> net = ffnet(conec); net.weights[:] = 1.
>>> net.derivative([0., 0., 0.])
array([[ 0.02233658,  0.02233658,  0.02233658],
       [ 0.02233658,  0.02233658,  0.02233658]])

randomweights()

Randomize network weights due to Bottou proposition.

If n is a number of incoming connections to the node, weights of these connections are chosen randomly from range (-2.38/sqrt(n), 2.38/sqrt(n))

sqerror(input, target)

Calculates sum of squared errors at network output.

Error is calculated for normalized input and target arrays.

Parameters:

input : 2-D array

Array of input patterns

target : 2-D array

Array of network targets

Returns:

err : float

0.5*(sum of squared errors at network outputs)

Note

This function might be slow in frequent use, because data normalization is performed at each call. Usually there’s no need to use this function, unless you need to adopt your own training strategy.

sqgrad(input, target)

Returns gradient of network error vs. network weights.

Error is calculated for normalized input and target arrays.

Parameters:

input : 2-D array

Array of input patterns

target : 2-D array

Array of network targets

Returns:

grad : 1-D array

Array of the same length as net.weights containing gradient values.

Note

This function might be slow in frequent use, because data normalization is performed at each call. Usually there’s no need to use this function, unless you need to adopt your own training strategy.

test(input, target, iprint=1, filename=None)

Calculates output and parameters of regression.

Parameters:

input : 2-D array

Array of input patterns

target : 2-D array

Array of network targets

iprint : {0, 1, 2}, optional

Verbosity level: 0 – print nothing, 1 – print regression parameters for each output node (default), 2 – print additionaly general network info and all targets vs. outputs

filename : str

Path to the file where printed messages are redirected Default is None

Returns:

out : tuple

(output, regress) tuple where: output is an array of network answers on input patterns and regress contains regression parameters for each output node. These parameters are: slope, intercept, r-value, p-value, stderr-of-slope, stderr-of-estimate.

Examples:

>>> from ffnet import mlgraph, ffnet
>>> from numpy.random import rand
>>> conec = mlgraph((3,3,2))
>>> net = ffnet(conec)
>>> input = rand(50,3); target = rand(50,2)
>>> output, regress = net.test(input, target)
Testing results for 50 testing cases:
OUTPUT 1 (node nr 8):
Regression line parameters:
slope         = -0.000649
intercept     =  0.741282
r-value       = -0.021853
p-value       =  0.880267
slope stderr  =  0.004287
estim. stderr =  0.009146
.
OUTPUT 2 (node nr 7):
Regression line parameters:
slope         =  0.005536
intercept     =  0.198818
r-value       =  0.285037
p-value       =  0.044816
slope stderr  =  0.002687
estim. stderr =  0.005853

Exemplary plot:

from ffnet import mlgraph, ffnet
from numpy.random import rand
from numpy import linspace
import pylab

# Create and train net on random data
conec = mlgraph((3,10,2))
net = ffnet(conec)
input = rand(50,3); target = rand(50,2)
net.train_tnc(input, target, maxfun = 400)
output, regress = net.test(input, target, iprint = 0)

# Plot results for first output
pylab.plot(target.T[0], output.T[0], 'o',
                        label='targets vs. outputs')
slope = regress[0][0]; intercept = regress[0][1]
x = linspace(0,1)
y = slope * x + intercept
pylab.plot(x, y, linewidth = 2, label = 'regression line')
pylab.legend()
pylab.show()

(Source code, png, hires.png, pdf)

train_bfgs(input, target, **kwargs)

Train network with constrained version of BFGS algorithm.

Parameters:

input : 2-D array

Array of input patterns

target : 2-D array

Array of network targets

maxfun : int

Maximum number of function evaluations (default is 15000)

bounds : list, optional

(min, max) pairs for each connection weight, defining the bounds on that weight. Use None for one of min or max when there is no bound in that direction. By default all bounds ar set to (-100, 100)

disp : int, optional

If 0, then no output (default). If positive number then convergence messages are dispalyed.

See also

scipy.optimize.fmin_l_bfgs_b optimizer is used in this method. Look at its documentation for possible other useful parameters.

train_cg(input, target, **kwargs)

Train network with conjugate gradient algorithm.

Parameters:

input : 2-D array

Array of input patterns

target : 2-D array

Array of network targets

maxiter : integer, optional

Maximum number of iterations (default is 10000)

disp : bool

If True convergence method is displayed (default)

See also

scipy.optimize.fmin_cg optimizer is used in this method. Look at its documentation for possible other useful parameters.

train_genetic(input, target, **kwargs)

Global weights optimization with genetic algorithm.

Parameters:

input : 2-D array

Array of input patterns

target : 2-D array

Array of network targets

lower : float, optional

Lower bound of weights values (default is -25.)

upper : float, optional

Upper bound of weights values (default is 25.)

individuals : integer, optional

Number of individuals in a population (default is 20)

generations : integer, optional

Number of generations over which solution is to evolve (default is 500)

verbosity : {0, 1, 2}, optional

Printed output 0/1/2=None/Minimal/Verbose (default is 0)

See also

See description of pikaia.pikaia optimization function for other parameters.

train_momentum(input, target, eta=0.2, momentum=0.8, maxiter=10000, disp=0)

Simple backpropagation training with momentum.

Parameters:

input : 2-D array

Array of input patterns

target : 2-D array

Array of network targets

eta : float, optional

Learning rate

momentum : float, optional

Momentum coefficient

maxiter : integer, optional

Maximum number of iterations

disp : bool

If True convergence method is displayed

train_rprop(input, target, a=1.2, b=0.5, mimin=1e-06, mimax=50.0, xmi=0.1, maxiter=10000, disp=0)

Rprop training algorithm.

Parameters:

input : 2-D array

Array of input patterns

target : 2-D array

Array of network targets

a : float, optional

Training step increasing parameter

b : float, optional

Training step decreasing parameter

mimin : float, optional

Minimum training step

mimax : float, optional

Maximum training step

xmi : array (or float), optional

Array containing initial training steps for weights. If xmi is a scalar then its value is set for all weights

maxiter : integer, optional

Maximum number of iterations

disp : bool

If True convergence method is displayed. Default is False

Returns:

xmi : array

Computed array of training steps to be used in eventual further training calls.

train_tnc(input, target, nproc=1, **kwargs)

Parameters:

input : 2-D array

Array of input patterns

target : 2-D array

Array of network targets

nproc : int or ‘ncpu’, optional

Number of processes spawned for training. If nproc=’ncpu’ nproc will be set to number of avilable processors

maxfun : int

Maximum number of function evaluation. If None, maxfun is set to max(100, 10*len(weights)). Defaults to None.

bounds : list, optional

(min, max) pairs for each connection weight, defining the bounds on that weight. Use None for one of min or max when there is no bound in that direction. By default all bounds ar set to (-100, 100)

messages : int, optional

If 0, then no output (default). If positive number then convergence messages are dispalyed.

Note

On Windows using ncpu > 1 might be memory hungry, because each process have to load its own instance of network and training data. This is not the case on Linux platforms.

See also

scipy.optimize.fmin_tnc optimizer is used in this method. Look at its documentation for possible other useful parameters.

Utility functions

ffnet.savenet(net, filename)

Dumps network to a file using cPickle.

Parameters:

net : ffnet

Intance of the network

filename : str

Path to the file where network is dumped

ffnet.loadnet(filename)

Loads network pickled previously with savenet.

Parameters:

filename : str

Path to the file with saved network

ffnet.exportnet(net, filename, name='ffnet', lang=None, derivative=True)

Exports network to a compiled language source code.

Parameters:

filename : str

Path to the file where network is exported

name : str

Name of the exported function

lang : str

Language to which network is to be exported. Currently only Fortran is supported

derivative : bool

If True a function for derivative calculation is also exported. It is named as name with prefix ‘d’

Note

You need ‘ffnet.f’ file distributed with ffnet sources to get the exported Fortran routines to work.

ffnet.readdata(filename, **kwargs)

Reads arrays from ASCII files.

Note

This function just calls numpy.loadtxt passing to it all keyword arguments. Refer to this function for possible options.

Pikaia optimizer

pikaia.pikaia(ff, n, ff_extra_args=(), individuals=100, generations=500, digits=6, crossover=0.85, mutation=2, initrate=0.005, minrate=0.0005, maxrate=0.25, fitnessdiff=1.0, reproduction=3, elitism=0, verbosity=0)

Pikaia version 1.2 - genetic algorithm based optimizer.

Simplest usage:

from pikaia import pikaia
x = pikaia(ff, n)

Parameters:

ff : callable

Scalar function of the signature ff(x, [n, args]), where x is a real array of length n and args are extra parameters. Pikaia optimizer assumes x elements are bounded to the interval (0, 1), thus ff have to aware of this, ie. probably you need some internal scaling inside ff.

By convention, ff should return higher values for more optimal parameter values (i.e., individuals which are more “fit”). For example, in fitting a function through data points, ff could return the inverse of chi**2.

n : int

Length of x. Note that you do not need starting point.

ff_extra_args: tuple

Extra arguments passed to ff.

individuals : int

Number of individuals in a population (default is 100)

generations : int

Number of generations over which solution is to evolve (default is 500)

digits : int

Number of significant digits (i.e., number of genes) retained in chromosomal encoding (default is 6). (Note: This number is limited by the machine floating point precision. Most 32-bit floating point representations have only 6 full digits of precision. To achieve greater precision this routine could be converted to double precision, but note that this would also require a double precision random number generator, which likely would not have more than 9 digits of precision if it used 4-byte integers internally.)

crossover : float

Crossover probability; must be <= 1.0 (default is 0.85). If crossover takes place, either one or two splicing points are used, with equal probabilities.

mutation : {1, 2, 3, 4, 5, 6}

digit	description
1	one-point mutation, fixed rate
2	one-point, adjustable rate based on fitness (default)
3	one-point, adjustable rate based on distance
4	one-point+creep, fixed rate
5	one-point+creep, adjustable rate based on fitness
6	one-point+creep, adjustable rate based on distance

initrate : float

Initial mutation rate. Should be small (default is 0.005) (Note: the mutation rate is the probability that any one gene locus will mutate in any one generation.)

minrate : float

Minimum mutation rate. Must be >= 0.0 (default is 0.0005)

maxrate : float

Maximum mutation rate. Must be <= 1.0 (default is 0.25)

fitnessdiff : float

Relative fitness differential. Range from 0 (none) to 1 (maximum) (default is 1).

reproduction : {1, 2, 3}

Reproduction plan; 1/2/3 = Full generationalreplacement/Steady- state-replace-random/Steady-state-replace-worst (default is 3)

elitism : {0, 1}

Elitism flag; 0/1=off/on (default is 0) (Applies only to reproduction plans 1 and 2)

verbosity : {0, 1, 2}

Printed output 0/1/2=None/Minimal/Verbose (default is 0)

Returns:

x : array (float32)

The ‘fittest’ (optimal) solution found, i.e., the solution which maximizes fitness function ff.

Examples:

>>> from pikaia import pikaia
>>> def ff(x): return -sum(x**2)
>>> pikaia(ff, 4, individuals=50, generations=200)
array([  1.23000005e-04,   7.69999970e-05,   2.99999992e-05,
 2.80000004e-05], dtype=float32)

Note

Original fortran code of pikaia is written by: Paul Charbonneau & Barry Knapp (paulchar@hao.ucar.edu, knapp@hao.ucar.edu)

Wrapped with f2py by Marek Wojciechowski (mwojc@p.lodz.pl)